我看另一个伟大的Numberphile上周的视频。在这布雷迪采访了马特·亨德森关于他更多迷人的数字可视化。在这种情况下集马特谈到了我们如何想象的无穷位数非理性的数字,例如π或φ(黄金比例),使用龟图还有一个很酷的钢笔绘图仪。
这让我想到了一些数学th我女儿最近一直在研究分数和小数展开,马特的一些想法是否能帮助她更好地理解这是怎么回事?至少,我希望关于数字的更直观的对话可能会激发人们对支撑数学的美丽模式的更深层次的欣赏……一个父亲可以梦想……
无论如何,在这篇文章中,我将描述我如何应用Matt的一些想法来开始我自己对数字视觉景观的探索。我决定专注于表单的简单分数1 / n这里我要看看的值n从1到100。我的目标是描述我使用的方法,并展示结果可视化,其中有一些最有趣的方面,但在大多数情况下,我将让可视化自己说话。
TMatt使用的可视化方法很简单,我在本文末尾包含了一个基本Python实现的代码片段。方法是这样的:
- 想象一下,我们正在控制一个小型机器人(turtle图形中的“海龟”),它能够在移动时绘制它所遵循的路径。
- 为了简单起见,这个机器人总是向前移动一个单位距离,我们想要可视化的数字的数字决定了它移动的方向。
- 因为有10个可能的数字(0,1,2,…,9),所以有10个可能的方向和数字d转换成的角度d * 360/10度。因此,数字1将使机器人从当前方向旋转36度,数字2将产生72度旋转,依此类推。
- 这样,任何数字都可以通过遵循编码在数字中的方向指示来可视化。数字也可以用来分配一个颜色的每个线段上的路径产生;10个数字有10种可能的颜色。
下面的动画展示了我们如何使用这种方法来可视化分数1/14(.0714285…)的十进制展开的前64位。1/14的十进制展开式是无穷大的,叫做a重复的部分或循环小数-数字714285永远重复,但不是每个分数都是重复的,我们会看到。每个连续的数字对应一个新的彩色编码线段。在这种情况下,前两位数字(00)导致两个水平(蓝色)线段,因为;转角为0。接下来,数字7 (7 x 36 = 252)会出现一个252度的急转弯,然后数字1会出现一个更温和的36度转弯,依此类推。

为了方便读者进行更轻松的分析,下面的序列显示了该动画的各个帧。在每一帧中,起始点由填充标记表示,结束点由未填充标记表示。每一帧也被标记为它对应的数字。

现在我们已经掌握了可视化过程,让我们看看将其应用到一些熟悉的分数上的结果。
下面是一个网格的所有部分的形式1 / n的值n从1到100。如果存在的话,每个图形可视化到十进制展开的前1000位;简单的无重复这样的分数1/2,1/4,等等都没有无限小数展开,因此只能为可视化贡献少量数字。如上所述,线段已被着色以反映数字和相应的转角,因此每个可视化的形状和颜色告诉我们关于十进制展开的数字。

当我第一次看到这些可视化时,我对它们在视觉上的有趣和引人注目印象深刻。我没想到像1/7这样的简单分数会产生如此对称的“螺旋桨”,看看1/83或1/98的可视化的复杂本质,它们看起来像精致的花环。

作为题外话,值得强调的是,所有这些可视化都被缩放以最大化易读性——通过确保它们填充可用的框架——但这掩盖了1/27可视化的结构,从表面上看,它看起来像一条简单的直线,表明一个非重复的分数。实际上,当我们放大其十进制展开的前100位时,这个分数具有更复杂的楼梯状可视化,如上图所示。
O显然,复杂的结构和旋转对称性在许多可视化中是显而易见的,因为它们的十进制展开具有周期性。它们反复出现的数字合谋创造了可视化中的重复结构。在数学语言中,这些无限重复的数字序列被称为重复的语句或reptends而一个reptend的长度被称为它期.
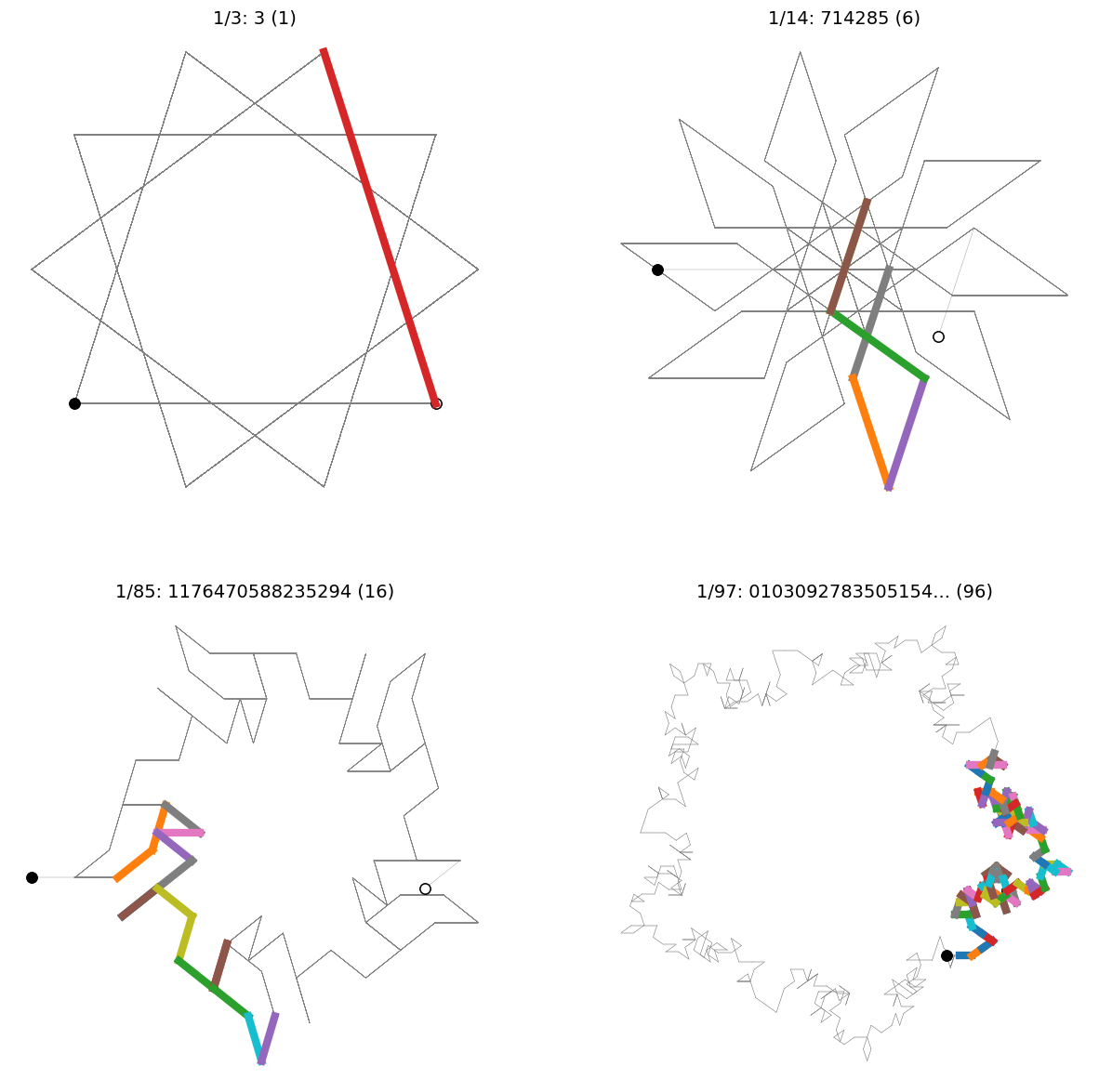
上面的四种可视化显示了分数1/3、1/14、1/85和1/97的十进制展开中的前1000位,以一种突出显示每个分数的重复数字的第一次出现的可视化部分的方式。
选择这些分数是因为它们有不同的重现期。1/3的重复是单个数字“3”(周期为1),这意味着它的可视化由与当前标题成108度角的单个线段(红色)的重复组成,如图所示。
分数1/14有一个6位数的reptend(' 714285 '),它可以翻译成一个个体。叶片的结果,10个叶片,螺旋桨风格的可视化。注意,对于1/14的6位数reptend,只有5个线段可见。这是因为它的最后一个数字“5”导致可视化转向自身(180度转弯),以掩盖之前的线段“8”。
时间越长,事情就越复杂。1/85的16位重复对应它的五边形可视化的一面,而1/97的96位重复创建了它的5个角片段之一。
F从可视化的角度来看,reptend的长度是衡量复杂性的有用指标,因为具有较长重复序列的分数往往比具有较短重复序列的分数产生更丰富的可视化效果。为了看到这一点,下面的图表按照它们的长度降序重新排列。此外,它们突出了与再现的第一次出现相对应的可视化部分。这有助于阐明每个可视化是如何由一组重复的组件组成的。

通常,这幅画对视觉化的贡献是直观的。例如,在分数中1/7而且1/14它对应于一个主要的叶片’和类似的1/19,它对应一个单一的'手臂的想象。然而,对于分数,如1/94,1/71而且1/62重复的结构远没有那么明显,实际上是以一种更复杂的方式编织在可视化中。
还要注意最好的分数(质数的倒数) - - -1/p, p是质数——与p > 5与非质数分数相比,与更长的再现和更大的可视化复杂性相关。我相信这是数论学家所熟知的。对于除2和5之外的任何质数p, 1/p的十进制展开重复一个除p-1的周期-但有趣的是,它也反映在可视化中,值得进一步研究。
T这篇文章的目的是开始一个简单的分数形式的视觉探索1 / n,通过使用十进制展开作为一组方向指令来指导可视化过程。我发现结果既引人注目,又吸引人,因为它们揭示了结构的丰富性和规律性。
我集中讨论了可视化和重复十进制展开的本质之间的关系。具有较长重复序列的分数与更复杂的可视化相关联,但到目前为止,我只触及了表面,还有很多值得进一步研究的地方:
- 为什么大多数可视化也会显示5倍或10倍旋转对称吗?大概是因为我用的是以10为底?对于较大的值,这种情况是否持续n或者是1 / n?在其他数字基础上,可视化是如何变化的?对称是否可以从十进制展开本身确定,也就是说不产生可视化?
- 显然,某些分数之间存在很强的关系。例如,基于3,6和7的倍数的分数是相似的,当然,10的倍数(1/n, 1/10n, 1/100n等)将产生几乎相同的可视化,除了由于任何额外的平移位移。0在小数点后。我们可以从这些关系中学到什么,它们是如何影响可视化的?
- 那么当我们组合分数时,加/减,乘/除会怎样呢?他们的可视化是否以可预测的方式变化?
- 有很明显不同类别的可视化,例如,星星,螺旋桨,五边形和十边形,楼梯等。这是完整的集合还是简单分数的其他可视化类别?
我最初的目标是帮助我的女儿更好地理解我们周围存在的数字模式……这是如何实现的?我们只能说这是一项正在进行中的工作。但从好的方面来看,至少可视化效果很受欢迎。在我们的家庭中,我们现在都有自己喜欢的分数,看到她的兴趣发展是值得的,因为她试图发现可视化中的重复结构,并将它们与十进制展开的数字相匹配。
附录
下面的Python代码片段包含为给定数字生成可视化的代码。在这项工作中,我使用Matplotlib来制作图像和Mpmath对于所要求的浮点精度;Python的默认精度是不够的。
Def draw_number(ax, n):
"""为一个数字n画一个简单的图。
参数:
ax:用于可视化的轴(Matplotlib)。
N:要想象的数字。
”“”#将n转换为数字字符串;去掉小数点。
数字= tr(n).replace('。“,”)坐标=[(0,0)]#起始坐标。
航向= 0 #偏东航向。#遍历每个数字…
对于双位数:#将数字转换为所需进位的int型。
N = int(数字)#使用数字选择转弯角度;假设底数为10。
度= n*360/10
#用新的角度更新当前标题
标题+ =度#当前的x, y坐标。
Current_x, current_y =坐标[-1]
#根据新标题计算x和y偏移量。
X_offset = math.cos(math.pi*heading/180)
Y_offset = math.sin(math.pi*heading/180)
#新的x和y坐标。
New_x, new_y = current_x + x_offset, current_y + y_offset
#绘制从当前到新xy的新线
ax.plot ([current_x, new_x], [current_y, new_y])#添加新的xy到坐标列表。
坐标。追加((new_x new_y))
#标记起点和终点
ax.plot (
(坐标[0][0])* 2(坐标[0][1]]* 2,
Marker ='o', markersize=8, markeredgecolor='k', color='k'
)
ax.plot (
(坐标[1][0])* 2(坐标[1][1]]* 2,
Marker ='o', markersize=8, markeredgecolor='k', color='w'
)返回已绘制的坐标。
返回坐标








